The last few years have brought us incredible advancements in machine learning. These diverse systems are built from a few core building blocks, which are modified and combined in complex ways.

These core ideas often get abstracted away when discussing the bigger picture, which leaves us to wonder — “What’s going on inside?”

In this interactive lesson, we will answer that question by thinking small.

We will start with the simplest of models — The Line, and see how it can help us build a Neural Network capable of learning anything. Then, going back to the line, we will learn how to train it using the Gradient Descent algorithm, which we will write from scratch in Python.

Modelling Our World

The power of machine learning lies in its ability to distill down large volumes of data into useful representations we call models.

Think of models like play dough. They have adjustable parameters which let us mold them into various shapes. Training is the process of molding them based on data.

Weights and Biases

The line is one of the simplest of models with just two parameters. The weight $w$ controls the line’s tilt and the bias $b$ shifts it.

By the way, we will label inputs as $x$ and outputs as $y$.

We can generalize this to multiple inputs $x_1, x_2, ... x_n$:

Notice that each input $x_i$ gets scaled by its own weight $w_i$.

By adjusting these weights, we can tune how much each input influences the value of $y$.

The bias $b$ is independent of any input, it simply shifts $y$ towards the positive or negative direction.

We can see this in action by plotting a linear model with two inputs, $y(x1, x2)$.

Activation Functions

The linear model is… well, linear. But not everything in our world is described in straight lines.

Here’s a non-linear function known as the sigmoid $\sigma$.

It smoothly transitions from $0$ to $1$.

Something interesting happens when we pass a linear model into the sigmoid: $\sigma(wx + b)$.

We are able to use the $w$ and $b$ parameters of the line to change the sharpness and center of the sigmoid’s transition!

This has transformed our line into something like an on-off switch, where we can control the threshold with $b$ and represent uncertainty with $w$.

Functions like the sigmoid into which we pass our linear model are known as Activation Functions. There are many of them out there, of which the sigmoid is the most classic example.

Like before, we can extend this to multiple inputs:

Here’s $y(x_1, x_2) = \sigma(w_1x_1 + w_2x_2 + b)$:

If we view it from the top, we see that the activated and non-activated regions are split by a linear boundary.

The model we’ve just created takes in the values of its inputs, scales them by their weights, sums these results with the bias and then feeds the sum into the sigmoid, which then decides whether to activate or not.

In structure, this is similar to a biological neuron. Dendrites on the neuron’s body receive inputs from other neurons. Based on this, the neuron decides whether it should fire a signal through its axon, to which more neurons may be connected. These connections can grow stronger, analogous to the weights in artificial neurons.

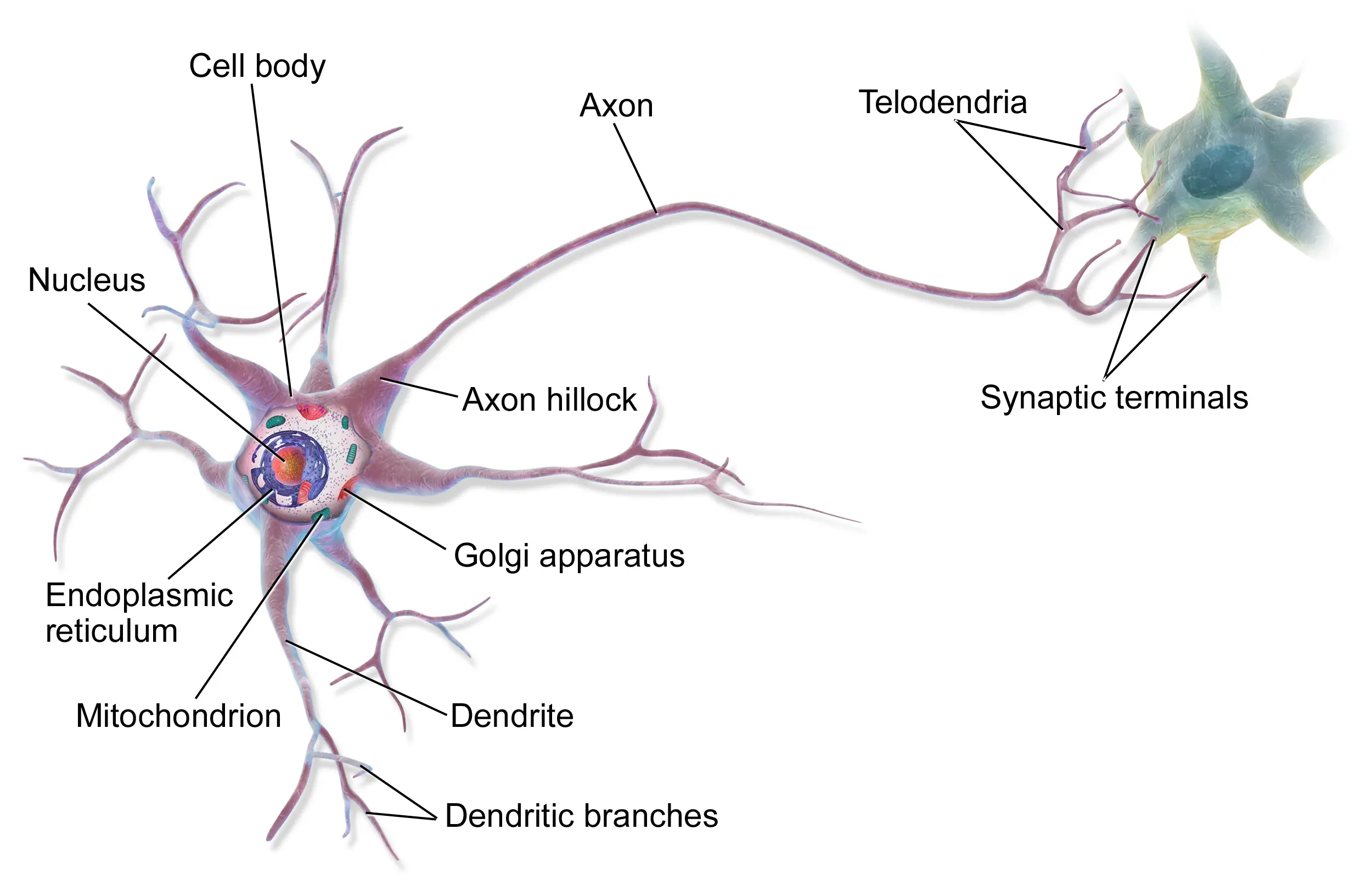Image credit: Wikipedia.

Neural Networks

Like biological neurons, we can treat the outputs of artificial neurons as inputs for other neurons.

Here’s a setup where $y$ is a special output neuron (we give it no activation function). Its input is the output of the previous neuron in the chain, this connection has an adjustable weight.

Tweaking this weight allows us to scale the range of the sigmoid function, so it’s no longer confined between $0$ and $1$!

But we can go further, and add neurons in parallel. Here’s two of them.

They stack on top of each other. What if we add more neurons?

This network can draw some variety of functions!

In fact, if we add more neurons, we’re able to draw more intricate functions.

And here, we’ve come face-to-face with what makes Neural Networks so powerful. As long as we have enough neurons in the middle layer, we can mold our network to the shape of any arbitrary function we like, to the level of accuracy we need. They are Universal Function Approximators.

And this all began with the humble line.

The rest of this article focuses on the training process. To keep us focused, will use the line as our model, but these ideas apply to all the other models we’ve seen.

Creating a model in code

The code block below plots $y(x) = x$. I’d like you to update this function to plot $y(x) = wx + b$ by using the w and b variables already defined. Once done, click on “Run” and you should be able to use the sliders to control the weight and bias of the line.

b = 0
w = 1

def y(x, w, b):
  return x

Great! We now have a model which can fit to some data.

Fitting a model to data

Our data will exist as $(x, y)$ pairs. Where $x$ is the value of some input variable, and $y$ is the corresponding output of that variable.

This data could represent anything!

• Maybe you want to predict how many ice-creams you can sell $(y)$ based on the current temperature $(x)$.
• Or how much energy your solar panels can generate $(y)$ based on the hours of daylight $(x)$.
• Or if you’re Sherlock, how tall a person is $(y)$ based on the length of their footprint $(x)$.

In all these cases, we can reasonably assume that $x$ and $y$ are roughly linearly related. Knowing this, we can choose to use our linear model to fit to this data.

Data from the natural world will have randomness, our variables may also not be linearly related throughout (maybe ice-cream sales start off linearly, but plateau beyond a certain point). We should be aware of a model’s limitations when we use it.

To keep things simple, we will use some made-up data for our program. But you may edit it as you wish!

Now, can you use the sliders to find the values of $w$ and $b$ that best fit this data?

data = [(1, 0.85), (2, 1.43), (3, 1.92), (4, 2.59), (5, 3.20), (6, 3.82), (7, 4.38), (8, 4.97)]

w = 1
b = 0

def y(x, w, b):
  return w * x + b

Great! The values of $w$ and $b$ you have found, are now a condensed representation of our data points, which we would no longer require. We can instead feed their $x$ values into our trained model and get approximately the same $y$ values out of it.

x_values = [1, 2, 3, 4, 5, 6, 7, 8]
data = []

w = 0.6
b = 0.2

def y(x, w, b):
  return w * x + b

for xi in x_values:
  data_point = (xi, y(xi, w, b))
  data.append(data_point)

But now we can do more, and also predict $y$ for values of $x$ that were not in our data!

x_values = [-3, 6.28]
data = []

w = 0.6
b = 0.2

def y(x, w, b):
  return w * x + b

for xi in x_values:
  data_point = (xi, y(xi, w, b))
  data.append(data_point)

This is how a trained model is useful. Not only are we storing a more compact representation of the data through its parameters, but we can also get predictions for inputs it never saw before.

This is also true for neurons and neural networks. Which may have more inputs, and more parameters to model a variety of shapes.

Our next step will be to figure out how to train the model automatically.

The Loss Function

When you fit the line to the data points in the previous section, you were able to visually see how well they were aligned.

But machines don’t see, they crunch numbers. So we need a way to quantify how well the model matches its data.

For any single data point $(x_i,y_i)$, we can measure the absolute difference between the output $y_i$ and the model’s prediction based on the current values of $w$ and $b$, $y_{w,b}(x_i)$.

Then we can sum these up for every data point.

We have just created a Loss Function, this one is known as $L1$ loss.

As an alternative to the $|modulus|$ function, we can also $square^2$ the difference. This gives us the Loss Function named $L2$ loss and it has a couple of advantages:

1. Unlike the modulus function, the square function is differentiable at all points, and we will need that for the Gradient Descent algorithm.
2. Since the error gets squared, data points that are way off get penalized a lot more than those which are closer to the line.

The $\frac{1}{2}$ factor will just make things convenient when computing derivatives!

Let’s see our loss function in action!

data = [(1, 0.85), (2, 1.43), (3, 1.92), (4, 2.59), (5, 3.20), (6, 3.82), (7, 4.38), (8, 4.97)]

w = 1
b = 0

def loss():
  sum = 0
  for xi, yi in data:
    sum += (y(xi, w, b) - yi) ** 2
  return sum / 2

def y(x, w, b):
  return w * x + b

The Loss Landscape

The Loss Function’s inputs are our model’s parameters — $w$ and $b$. We can create a plane, with a $w$-axis and a $b$-axis. Picking any point on this plane would give us a combination of $(w,b)$ which can be used to represent a unique line.

This plane is our model’s parameter space. We can compute our Loss Function for every point on it, and plot the output on a third axis.

This visualization is known as the Loss Landscape of our model.

data = [(1, 0.85), (2, 1.43), (3, 1.92), (4, 2.59), (5, 3.20), (6, 3.82), (7, 4.38), (8, 4.97)]

w = 1
b = 0

def loss(w, b):
  sum = 0
  for xi, yi in data:
    sum += (y(xi, w, b) - yi) ** 2
  return sum / 2

def y(x, w, b):
  return w * x + b

After plotting the Loss Landscape, we can easily see that there’s a point where the loss is the lowest.

Our job in the next steps will be to develop an algorithm which descends along the Loss Landscape to reach the bottom of this valley from any starting position, without computing every point on the Loss Landscape.

For this, we would need a way for our machines to know which way is down…

Gradients: Which way is down?

Derivatives

This section assumes knowledge of Derivatives. We’ll quickly see how they’re useful to us.

Here’s a roller-coaster of a polynomial $f(x)$. If we draw a line tangent to it at some value of $x$, we see that this tangent has a changing slope.

slope of tangent: 1.3000

Since this slope depends on $x$, we can create a function that takes in $x$ and returns the slope of the tangent. That function is known as the derivative of $f(x)$.

Derivatives are usually written in the forms $\frac{df}{dx}$ or $f'(x)$, where $f$ is the original function and $x$ is the variable we are sliding.

How is this useful? Well, let’s use the widgets above to play a simple game:

1. Pick a random value of $x$ to start with.
2. If the slope is positive, move the slider slightly to the left.
3. If instead it is negative, move it to the right.
4. Repeat the last two steps, and you will always end up in a “valley” of the graph.

This works because the derivative always tells us which direction the function is increasing in. By going in the opposite direction (going left when the slope is positive), we always head downhill.

That’s exactly what we’re looking to do with our Loss Function too! But we still have one problem: our Loss Function $L_2(w,b)$ has two inputs, not one.

So we will need to do something clever about that.

Partial Derivatives

If we fix one of the inputs to some constant, say $L_2(w, b = 1)$, then we’ve converted our two-variabled Loss Function into a single variable function, because we can only adjust the other variable ($w$).

This would allow us to compute the derivative of this function like any other single variabled function.

Partial Derivatives are based on this idea. Except, the other variables are only treated as constants, and are not actually set to any numeric value.

We will instead set them to specific constants when we are evaluating the slope!

Our Loss Function $L_2(w,b)$ has two variables, and thus, two partial derivatives, $\frac{\partial L_2}{\partial w}$ and $\frac{\partial L_2}{\partial b}$.

Let’s say we are at a point $(w,b) = (2,1)$. Then evaluating $\frac{\partial L_2}{\partial w}$ here will fix $b$ (the variable we are not differentiating) to $b=1$, giving us a single variable function of $w$. The slope along the $w$ axis is returned for $w=2$.

Similarly, $\frac{\partial L_2}{\partial b}$ will give us the slope along the $b$ axis at the same point $(2,1)$.

When we combine both of these partial derivatives into a single vector, we call that vector the Gradient Vector $\nabla L_2(w,b)$.

The Gradient is to our Loss Landscape what the slope was to the polynomial. Imagine standing on the side of a hill. The Gradient tells you which direction is downwards, and how steep the ground beneath your feet is.

Computing the Partial Derivatives for our Loss Function

Here’s our Loss Function again:

We will need to find the partial derivatives for both $w$ and $b$. Let’s start with $w$ first.

The summation $\sum$ operator can make things messy. Since the derivative of a sum is equal to a sum of the derivatives, let’s put this operator outside the partial differentiation step.

Now, we could go ahead and differentiate this directly, but there is an easier way out, which scales well for more complex models.

A worthy observation is that we are differentiating a composite function, i.e. a function within a function.

I’ve written the outer function in $\color{blue}blue$ and the inner one in $\color{orange}orange$.

When we need to find derivatives of composite functions, we can use a property known as the Chain Rule to do this in a clean way.

The Chain Rule

Here’s the property. Let’s say we have two functions $h(x)$ and $g(x)$, and we use them to create a composite function $f(x)$:

The Chain Rule says that we can get the derivative $\frac{df}{dx}$ in the form of this product:

Here, $\frac{dg}{dx}$ is simply the regular derivative of $g$. But what is $\frac{dh}{dg}$?

Let’s say $h(x)$ was equal to $x^2$, then $\frac{dh}{dx}$ would be $2x$.

But with $h(g(x))$, the input to $h$ is now $g(x)$ instead of just $x$. So the derivative of $h$ with respect to this new input is written as $\frac{dh}{dg}$ and is computed to be $2g(x)$. We just replaced the $x$ in $2x$ with a $g(x)$.

This is helpful, because it’s easy to know the derivative of $g(x)$ or $h(x)$ individually. But to compute these derivatives for $h(g(x))$ would be much more involved. The chain rule helps us take a shortcut by using the atomic derivatives instead.

Let’s apply the Chain Rule on our Loss Function.

Note that we are naming $L_2$ to be the outer function $\color{blue}\frac{1}{2}(\color{black}x\color{blue})^2$. We can ignore $y_i$ here, because it is a constant which gets dropped during differentiation.

So we have to find $\frac{\color{blue}\partial L_2}{\color{orange}\partial y_{w,b}(x_i)}$ and $\frac {\color{orange}\partial y_{w,b}(x_i)}{\partial w}$. Let’s start with the latter.

Recall the equation of the line $y_{w,b}(x)$:

When we’re computing the partial derivative with respect to $w$, it remains a variable and everything else ($x, b$ in this case) is treated to be a constant. Therefore, we get:

Now let’s work with the other part, $\frac{\color{blue}\partial L_2}{\color{orange}\partial y_{w,b}(x_i)}$. Our outer function is $\frac{1}{2}x^2$. It’s derivative is $\frac{d}{dx} \frac{1}{2}x^2 = \frac{1}{2}2x$, which simplifies to just $x$, the input. In our case that looks like this:

We’ve computed both parts from the chain rule, let’s multiply them together:

And we have the partial derivative for $w$! Now we do the same for $b$.

We previously computed the first part to be $y_{w, b}(x_i) - y_i$. Let’s look at the second:

Now we multiply the two together:

We now have the partial derivatives for our two parameters! Let’s package them into the Gradient Vector.

Let’s try to visualize the Gradient vector on the Loss Landscape. Remember that we had moved the summation operator aside, we will need to add that back.

data = [(1, 0.85), (2, 1.43), (3, 1.92), (4, 2.59), (5, 3.20), (6, 3.82), (7, 4.38), (8, 4.97)]

w = 1
b = 0

def loss(w, b):
  sum = 0
  for xi, yi in data:
    sum += (y(xi, w, b) - yi) ** 2
  return sum / 2

def gradient():
  dw = db = 0
  for xi, yi in data:
    dw += (y(xi, w, b) - yi) * xi
    db += y(xi, w, b) - yi
  return dw, db

def y(x, w, b):
  return w * x + b

We see that the Gradient Vector is incredibly large. This is because of the steepness of the Loss Landscape. You can try to reach to the shallower regions and see the vector change size and direction.

What is useful for us is that it points in the right direction, if the point moves that way by a very small amount.

Steps in the Right Direction

We will now try to use the information in the Gradient Vector to update our model’s parameters!

Since as we just saw, the size of this vector is gigantic, we will scale it down by a factor. This is normally known as the learning rate or the step size.

Then we will update the parameters to where the scaled gradient vector tells us to go.

The choice of the learning rate is critical here. Too low, and the steps will be too small to reach our goal in a reasonable time. Too high, and our steps may overshoot our goal.

In the next code block, I’ve added a learning_rate variable. But I think I set it too high!

Can you try to find a good learning rate for our data?

data = [(1, 0.85), (2, 1.43), (3, 1.92), (4, 2.59), (5, 3.20), (6, 3.82), (7, 4.38), (8, 4.97)]

w = 1
b = 0

def loss(w, b):
  sum = 0
  for xi, yi in data:
    sum += (y(xi, w, b) - yi) ** 2
  return sum / 2

def gradient():
  dw = db = 0
  for xi, yi in data:
    dw += (y(xi, w, b) - yi) * xi  
    db += y(xi, w, b) - yi
  return dw, db

def y(x, w, b):
  return w * x + b

learning_rate = 0.01

def update():
  dw, db = gradient()
  global w,b
  w -= dw * learning_rate
  b -= db * learning_rate

You know you’ve found a good learning rate when the model starts to find stability in its movement after quickly getting closer to matching the data.

Great! We are able to get our model to fit closer to the data, a step at a time! Now we just need to have it make these steps automatically!

The Gradient Descent Algorithm

The new train() function will be called by the controls below. Normally, models are trained for a fixed number of iterations, but in this case the parameter iterations is instead being used to control the speed of the animation.

To finish it off, I’d like you to call the update() function inside its for loop. :)

data = [(1, 0.85), (2, 1.43), (3, 1.92), (4, 2.59), (5, 3.20), (6, 3.82), (7, 4.38), (8, 4.97)]

w = 1
b = 0

learning_rate = 0.001

def y(x, w, b):
  return w * x + b

def gradient():
  dw = db = 0
  for xi, yi in data:
    dw += (y(xi, w, b) - yi) * xi  
    db += y(xi, w, b) - yi
  return dw, db

def update():
  dw, db = gradient()
  global w,b
  w -= dw * learning_rate
  b -= db * learning_rate
  return w, b

iteration_counter = 0
def train(iterations = 100):
  global iteration_counter
  for i in range(iterations):
    # call update() in this loop!
    
    iteration_counter += 1

We’ve done it!

It’s just the beginning…

We’ve finally seen how machine learning models can be trained, and we’ve learnt this in detail by focusing on a simple model.

There are many paths from here. We can extend our code to multiple variables, or add an activation function, or even do both to create neural networks. We can also try different kinds optimization techniques.

Perhaps, you can train a model for some data that interests you!

Whatever that may be, I hope that you keep learning more about this fascinating subject!

Thank you for reading!

This lesson is an entry for the Summer of Math Exposition 4. Every year, it brings together a variety of math content to love! Go check them out!

While you’re at it, I want to mention Jumplion’s entry where he uses math to find The Best Phonetic Alphabet. I helped him out in a step of the audio analysis part.